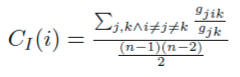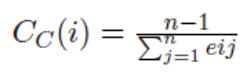Algumas Métricas de Análise em Redes Sociais
Algumas Métricas de Análise em Redes Sociais
O foco principal da Análise de Redes Sociais – ARS é a análise das relações que os indivíduos estabelecem entre si.
Neste sentido, a ARS dispõe de um conjunto de métricas que auxiliam na compreensão da dinâmica dos relacionamentos existentes nas redes analisadas. Dentre elas, destacam-se as métricas de Centralidade (Centrality), que permitem a avaliação da importância de um nó (individuo/ação/postagem) dentro da rede.
Nesse post verificaremos três Métricas de Centralidade propostas por Freeman (1978), a saber:
1. Centralidade de Grau
2. Centralidade de Intermediação
3. Centralidade de Proximidade.
Além das Métricas de Centralidade, serão verificadas também as Métricas de Autoridade e Grau Ponderado. As definições das mesmas podem ser observadas a seguir:

onde “n” é o número de nós, “gjk” é o número de caminhos mais curtos do nó “j” para o nó “k”, e “gjik” é o número de caminhos mais curtos de nó “j” para o nó “k” que passam pelo nó “i”. Esta métrica permite analisar o potencial de comunicação de um ator dentro da rede (Silva et al 2008).
C. Centralidade de Proximidade (Closeness Centrality): mede o comprimento médio dos caminhos mais curtos de um vértice para cada um dos outros vértices de um grafo. A centralidade de proximidade de um vértice “i” é calculada pela Equação 3.
onde “n” é o número de nós e “eij” é o número de arestas existentes no caminho mais curto do nó “i” para o nó “j”. Esta métrica indica a capacidade de alcance de um nó dentro da rede (Chelmis e Prasanna, 2011).
D. Grau Ponderado (Weighted Degree): É definida por Abbasi e Altmann (2011) como a soma de todos os pesos das arestas ligadas a um nó, sendo expressa pela Equação 4.
onde “n” é o número de nós, “wij” representa o peso da aresta entre o nó “i” e o nó “j”, ou seja, representa a quantidade de vezes que os dois nós se relacionaram. Tal métrica evidencia a força das relações entre os atores.
E. Autoridade (Authority): o valor de autoridade é calculado somando-se a quantidade de hubs com o qual o nó em questão está conectado. Seu cálculo é feito através do Algoritmo HITS, proposto por Kleinberg (1998). A Equação 5 descreve como se obtém a autoridade de um nó dentro da rede, onde “h” representa o número de hubs.
No contexto das redes de colaboração, as métricas mencionadas permitem entender a influência de um (individuo/ação/postagem) dentro de sua rede social de pesquisa. Apesar de existirem diversas outras métricas de ARS, os conceitos acima já proporcionam uma razoável compreensão de uma rede.